贝塞尔曲线
贝塞尔曲线是一个很牛X的东西。如果你玩过 Flash 或者 Photoshop,那么你肯定知道里面的钢笔工具,其实钢笔工具画出来的曲线就是贝塞尔曲线。
在数学的数值分析领域中,贝兹曲线,又称贝赛尔曲线(Bézier curve)是电脑图形学中相当重要的参数曲线。
贝塞尔曲线于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发,以稳定数值的方法求出贝塞尔曲线。
详细的公式请参考维基百科。
除了在汽车方面的应用,贝塞尔曲线还被用在字体设计方面。在 PC 上广泛使用的 TrueType 字体使用2阶贝塞尔曲线,字体上每个弧线使用3个点来表示,即使字体被放大好多倍,也能平滑地显示或印刷出来。而苹果使用了3阶贝塞尔曲线的 PostType 技术,每个弧线使用4个点来表示,所以苹果系统在设计和印刷方面比 PC 领先得多,浏览器中显示的字体也比 PC 要漂亮。
¶构造方式
贝塞尔曲线由两端的端点和中间的数个控制点来构造。两个端点确定了贝塞尔曲线起始和结束的位置,而控制点表示在曲线从起点到终点的过程中,移动的趋势或者方向。与曲线插值不同的是贝塞尔曲线几乎不经过控制点(在交叉的特殊情况也是有的)。以下这个动态图很直观的展示了它的构造过程。
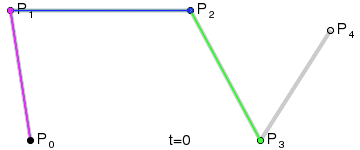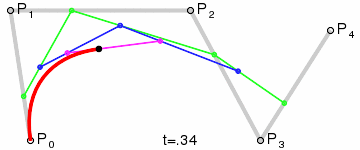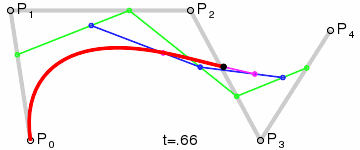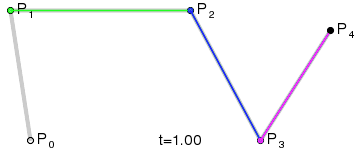
稍微改动一个控制点,整个贝塞尔曲线就会产生变化,有一种牵一发而动全身的感觉,所以很难对贝塞尔曲线进行微调。通常要调整多个控制点,或者断开原本的曲线,或者增加新的控制点。(可以参见 Photoshop 钢笔工具操作指南。)
不过这并不会阻挡我们对美好事物的向往,以下是我用 Processing 做的一个由5个动点构成的4阶贝塞尔曲线(准确的说是曲线上的点 :D)演示:
实际上我们并不在意如何修改控制点,只想静静地欣赏这个随风飘动的漂亮曲线。
Update: 20140417
在 Paper.js 里有一个很有意思的例子,关于曲线化简:它使用分段三次贝塞尔曲线拟合所给的样本点,产生极少数贝塞尔曲线端点和控制点构成的近似曲线。相关的论文可以参考 Graphic Gems 的这篇文章。
Update: 20200911
记录两个非常棒的贝赛尔曲线交互教程: