Jul 05, 2020 project

动森二维码生成器：服装类（后篇）

前篇写到动森二维码生成器的二维码划分规则以及预览模型的 UV 贴图。根据我的设想，接下来我要在 Aseprite 画板上将这个模型渲染出来，并将用户绘制的图案通过 UV 贴图的方式绘制到模型上。而目前我所拥有的东西只有：调整过 UV 贴图坐标的 6 个衣服模型、在 Aseprite 读取和写入像素的 Lua API，还有记忆中模糊的图形学知识。本文简单记录一下我当时的思路，以及遇到的一些细节问题，如果对实现有兴趣，可以直接访问 Github 上的该项目。

我做的第一件事是把模型从 Blender 中导出。因为我需要直接从 Lua 脚本读取模型的三角形顶点坐标、贴图坐标、法线向量。所以我选择了比较简单的 Wavefront(.obj) 格式，这种格式用很简单的语法来描述整个模型：

o model-name
v x0 y0 z0
v x1 y1 z1
v x2 y2 z2
...
vt u1 v1
vt u2 v2
vt u3 v3
...
vn nx0 ny0 nz0
vn nx1 ny1 nz1
vn nx2 ny2 nz2
...
f 1/1/1 2/2/2 3/3/3
...

其中 o 表示模型名字；v 表示顶点坐标；vt 表示贴图坐标；vn 表示法线向量；f 表示三角形面，三个顶点各自引用 v/vt/vn 的索引；.obj 格式如此简单，以至于不需要写很复杂的解释器，我直接用一个 Lua 脚本将其转换成 Lua 表文件，方便后期使用的时候直接加载。

不过在导出的时候需要注意坐标系系统。Blender 是 Z 轴向上的左手坐标系（X 轴向右，Y 轴向里），但 .obj 格式使用的是右手坐标系。所以在 Blender 导出的时候需要选择相应的变换规则（Up 轴和 Forward 轴），使得模型保持正确的方向。

接下来我将使用与 OpenGL 相同的坐标系：即 Y 轴向上，X 轴向右，Z 轴向外的右手坐标系。于是在 Blender 导出模型的时候选择 +Y Up, -Z Forward（按我的理解，这里的 -Z Forward 是以左手坐标系为准，即右手坐标系的 +Z Forward，非常 Tricky）。

注意这些选择会影响后面构建矩阵以及法线方向等细节。这对于从零实现渲染器来说相当重要。

有了模型数据，我们可以开始着手实现渲染器，将其绘制到画面中。这些衣服模型每个只有大概 1000 个三角形面，并且目标绘制的画面只有 256x256 像素。所以我只需要一个非常简易的 Rasterization 算法，甚至不需要优化。

简单地描述这个算法就是：遍历模型中的所有三角形，将顶点坐标除以 z 轴（简单透视）然后计算 BoundingBox(边界框)，遍历框中所有的点，看看它在不在三角形内，如果在，就在该点绘制相应的颜色，并记录其 z 坐标（若之后再绘制到该位置的点，则比较 z 坐标是否更靠近视角，是则覆盖）以解决可见性问题。

bounding-box-scan

这个过程中最漂亮的算法就是「点在三角形内」的判定。大前提：边的顶点需要满足在右手坐标系中逆时针排列（这在模型导出时就确定了）。则如果有一点在所有边的右侧，则它在三角形内，否则在三角形外。

那么要如何判定一个点在边的右侧呢？其实有好多方法，我举两个例子。若有线段AB和点P：

方法一：可以通过计算 XY 平面上的 AB×AP (crossProduct)，得到 Z 轴为正数则点在线段右侧（右手定则），该结果有很多含义，例如其方向为AB与AP的法向量，大小为AB与AP围成的三角形的面积的两倍。
方法二：计算线段AB的法向量与AP的夹角的余弦值（dotProduct)，得到正数则点在线段右侧。

相比之下方法一更为简单，也更容易实现。于是我用 Lua 简单实现了上述三角形栅格化算法，效果如下：

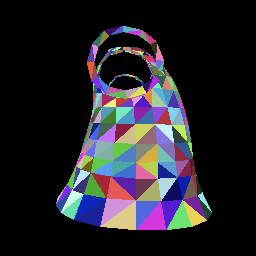
rasterization

上图为将模型中的所有三角形渲染渲染到画面上的结果。不过现在还没有加入模型的变换矩阵、相机矩阵等所以只能从固定角度得到画面。接下来，我们可以构建一个旋转变换矩阵，并应用到模型的每一个顶点上，这样模型就旋转起来了。

为了节省工作量，我找到了 LuaMatrix 这个开源库，可以帮助完成矩阵运算。不过在构造第一个矩阵之前，还要考虑一个问题：要以何种方式使用矩阵？行向量×矩阵，还是矩阵×列向量。

有些教程为了方便书写，会使用行向量×矩阵（或称 Row-major），在表述坐标的时候直接横着写 $(x0, y0, z0)$。也有些教程为了符合相应环境的开发习惯，使用矩阵×列向量（或称 Column-major）的形式，直接竖着写：$\begin{pmatrix} x0\\ y0\\ z0\end{pmatrix}$ （可见这种写法比较占页面）所以有些文章会将其写成转置的形式： $(x0, y0, z0)^T$，不过表示的也是列向量。

当使用行向量×矩阵时，矩阵放在 × 号右侧，所得结果也是行向量。当使用矩阵×列向量时，矩阵放在 × 号左侧，所得结果也是列向量。并且由于计算顺序的关系这两种矩阵互为转置。所以当你没有搞清楚用的是行向量还是列向量的时候，不要傻傻地把前者的矩阵直接拿到后者使用，否者构造出来的矩阵会让你晕头转向。本文将以列向量的形式创建相应的矩阵。

在最终的实现上，我只需要模型以 Y 轴转动。而在右手坐标系上，以 Y 轴转动的正方向是从 Z 轴顺时针转向 X 轴，于是这个矩阵可以由最基本的 2D 旋转矩阵变形得到：

$$ R_y(\theta) = \begin{bmatrix} cos(\theta) & 0 & sin(\theta)\\ 0 & 1 & 0\\ -sin(\theta) & 0 & cos(\theta) \end{bmatrix} $$

然而在程序中我们将使用 4 阶仿射矩阵，比起 3 阶矩阵，它可以很方便地与其它矩阵（例如平移矩阵）合并，应用到坐标上相当于一次完成多种变换。需要注意的是，对顶点进行变换的时候，需要对三维顶点补一维，对应数值为 1: $(x0, y0, z0, 1)^T$

-- create rotation matrix on y axis
function rotateY(a)
    return matrix({
        { math.cos(a), 0, math.sin(a), 0 },
        { 0, 1, 0, 0 },
        { -math.sin(a), 0, math.cos(a), 0 },
        { 0, 0, 0, 1 },
    })
end

Aseprite 的插件接口比较简陋，我使用了两个按钮来控制旋转的角度，效果如下：

现在模型可以「旋转」起来了，不过由于当前视角处于 Y=0 的位置平视模型，这并不是一个很好的观看角度，模型渲染起来也比较突兀。接下来我们考虑引入一个相机矩阵，本质上这也是一个平移与旋转的仿射矩阵，不过奇妙的地方是，我们可以直接通视角和朝向来创建这个矩阵，而不是对模型进行奇怪的平转与旋转。另外相机矩阵可以应用到整个场景的所有物体上，非常方便。相机矩阵的描述如下：

$$ \begin{bmatrix} x_{right} & x_{up} & x_{forward} & x_{eye}\\ y_{right} & y_{up} & y_{forward} & y_{eye}\\ z_{right} & z_{up} & z_{forward} & z_{eye}\\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1} $$

可见其本质是一个坐标系的逆矩阵，可以把顶点原来的世界坐标变换到相机空间中，以相机为原点。又因为相机的朝向为 -Z 方向，所有在视野内的物体都具有负的 Z 坐标。大多的 OpenGL 函数库都会有这样一个 lookAt 函数，用于通过视坐标与物坐标生成视矩阵，其中参数中的 UP 轴一般为世界坐标的 UP 轴（可以理解成端着相机的人站立的竖直方向，对这个方向进行控制可以获得相机摇摆的效果），并不是最终相机空间的 UP 轴，相机的 UP 轴通过两次叉乘得到：

-- create a camera to world matrix
-- use matrix:inverse() to get the world to camera matrix
function lookAt(eye, target, up)
    local globalUp = up and normalize(up) or { 0, 1, 0 }
    local forward = normalize({ eye[1] - target[1], eye[2] - target[2], eye[3] - target[3] })
    local right = crossProduct(globalUp, forward)
    local up = crossProduct(forward, right)
    return matrix({
        { right[1], up[1], forward[1], eye[1] },
        { right[2], up[2], forward[2], eye[2] },
        { right[3], up[3], forward[3], eye[3] },
        { 0, 0, 0, 1 }
    })
end

稍微抬高视角，俯视模型，感觉比之前好一些：

目前，模型的三角形面已经成功渲染在画面上了。接下来我希望能将用 UV 贴图来填充三角形。前面的颜色是三角形面上的属性，绘制三角形的时候可以直接使用这个单一颜色，然而 UV 坐标则是顶点的属性，绘制三角形内部的点时，需要以三个顶点的 UV 坐标计算出这个点的 UV 坐标（即插值）。三角形内的点通常使用的插值方式是「重心插值（Barycentric Interpolation）」。不过这只能在仿射变换这类可以保证比例一致性的情况下使用。如果要对透视变换后的三角形顶点进行插值，还需要多一步「透视矫正插值（Perspective-Correct Interpolation）」。为了测试 UV 映射的计算，我将 uv 坐标直接映射到 rgb 空间，看看效果：

UV 映射的效果不错，接下来就是读取贴图，然后按插值手的 UV 坐标从贴图上读取颜色，绘制到三角形内：

虽然贴图已经正确绘制，但是渲染出来的效果给人一种很扁平的感觉。我觉得需要加一点光照效果，可以立模型立体起来。正好可以用到前面导出的法线。

模型的法线一样要经过旋转矩阵和相机矩阵的变换（因为我们是在视空间进行光照计算，所以法线不需要经过透视变换），但与顶点变换有一处不同：法线是一个向量，由于顶点可以被平移，而法线只有方向没有位置，所以在仿射空间中，向量的 w 为 0，而顶点的 w 为 1。当 w 为 0 的时候，仿射变换矩阵的第四列 $(t_x, t_y, t_z, 1)^T$ 不参与计算，也就不会被平移。

有了法线，我们可以简单计算法线与向相机的 Forward 向量（0, 0, 1) 的夹角来调整颜色的灰度。这样非常容易就可以实现卡通渲染（toon shading）的风格，很较适合这个项目，效果如下：

不过光看模版图片效果有点太朴素了。于是我临摹了一张四代火影的衣服，并生成预览。效果如下：

大功告成！